ಎರಡು ಬಿಂದುಗಳ ನಡುವಿನ ದೂರ ಮತ್ತು ಭಾಗ ಪ್ರಮಾಣ ಸೂತ್ರ
ಎರಡು ಬಿಂದುಗಳ ನಡುವಿನ ದೂರ ಮತ್ತು ಭಾಗ ಪ್ರಮಾಣ ಸೂತ್ರ
ಎರಡು ಬಿಂದುಗಳ ನಡುವಿನ ದೂರ
ಬಿಂದುಗಳನ್ನು ನಕ್ಷಾಹಾಳೆಯ ಮೇಲೆ ಗುರುತಿಸುವುದನ್ನು ನಾವು ಈಗಾಗಲೇ ಕಲಿತಿದ್ದೇವೆ. ಆಗಾಗ ಎರಡು ಬಿಂದುಗಳ ನಡುವಿನ ದೂರವನ್ನು( ಬಿಂದುಗಳನ್ನು ನೇರವಾಗಿ ಸೇರಿಸುವ ರೇಖಾಕಂಡದ ಉದ್ದ) ಕಂಡುಹಿಡಿಯಬೇಕಾಗುತ್ತದೆ.
|
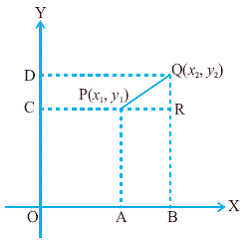
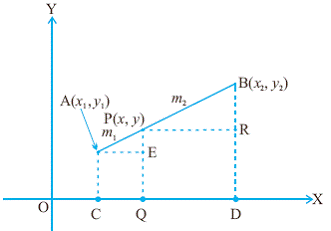
ಯಾವುದೇ ಬಿಂದುವನ್ನು x ಮತ್ತು y ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲಕ ಗುರುತಿಸಬಹುದು ಎಂದು ಕಲಿತಿದ್ದೇವೆ P (x1,y1) ಮತ್ತು Q (x2,y2) be the ಎರಡು ಬಿಂದುಗಳಾಗಿರಲಿ. ನಾವು PQ ರೇಖಾಖಂಡದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿದೆ. P ಮತ್ತು Q ಗಳಿಂದ X ಅಕ್ಷಕ್ಕೆ PA ಮತ್ತು QB ಎನ್ನುವ ಲಂಬಗಳನ್ನು ಕ್ರಮವಾಗಿ ಎಳೆಯಿರಿ. OA = x1 ಮತ್ತು OB = x2 ಎನ್ನುವುದನ್ನು ಗಮನಿಸಿ P ಮತ್ತು Q ಗಳಿಂದ Y ಅಕ್ಷಕ್ಕೆ PC ಮತ್ತು QD ಎನ್ನುವ ಲಂಬಗಳನ್ನು ಕ್ರಮವಾಗಿ ಎಳೆಯಿರಿ. OC = y1 ಮತ್ತು OD = y2 ಎನ್ನುವುದನ್ನು ಗಮನಿಸಿ. CP ಯನ್ನು ವಿಸ್ತರಿಸಿದಾಗ ಅದು BQ ಯನ್ನು R ನಲ್ಲಿ ಸಂಧಿಸಲಿ. PR = OB-OA = x2-x1 QR = OD-OC = y2-y1 PRQ ಎನ್ನುವುದು ಲಂಬಕೋನತ್ರಿಕೋನವಾಗಿರುವುದರಿಂದ ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯದಂತೆ PQ2 = PR2+RQ2= (x2-x1)2+ (y2-y1)2 PQ = {(x2-x1)2+ (y2-y1)2} ಇದನ್ನೇ ದೂರದ ಸೂತ್ರ('Distance formula') ಎಂದು ಕರೆಯುತ್ತೇವೆ. |
|
ಉಪಪ್ರಮೇಯ : ಒಂದು ಬಿಂದು ಮೂಲಬಿಂದು(0,0) ಆದರೆ ಸೂತ್ರ ಏನಾಗುತ್ತದೆ?
ಆಗ ಮೂಲಬಿಂದುವಿನಿಂದ O(0,0) P (x,y) ಗೆ ಇರುವ ದೂರ OP = (x2+ y2)
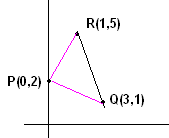
ಸಮಸ್ಯೆ 1: P(0,2) ಬಿಂದುವು Q(3,k) ಮತ್ತು R(k,5) ಬಿಂದುಗಳಿಂದ ಸಮಾನದೂರದಲ್ಲಿದ್ದರೆ k ಯ ಬೆಲೆ ಕಂಡುಹಿಡಿ.
ಪರಿಹಾರ:
|
PQ = {(3-0)2+ (k-2)2} = (9 +k2-4k+4) PR = {(k-0)2+ (5-2)2} = ( k2+9) PQ=PR ಆಗಿರುವುದರಿಂದ 9 +k2-4k+4 = k2+9 ಇದನ್ನು ಸುಲಭೀಕರಿಸಿದಾಗ k = 1
P(0,2) ಬಿಂದುವು Q(3,1) ಮತ್ತು R(1,5) ಬಿಂದುಗಳಿಂದ ಸಮಾನದೂರದಲ್ಲಿದೆ. |
|
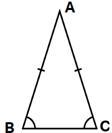
ಸಮಸ್ಯೆ 2: A(10,-18), B(3,6) ಮತ್ತು C(-5,2) ಮೂರು ಬಿಂದುಗಳಿಂದ ಉಂಟಾಗಿರುವ ತ್ರಿಕೋನದ ವಿಶೇಷತೆ ಏನು?
ಪರಿಹಾರ:
|
AB = {(3-10)2+ (6-(-18))2} = (49+ 576) = (625) =25 AC = {(-5-10)2+ (2-(-18))2} = (225+ 400) = (625) =25 BC = {(-5-3)2+ (2-6)2} = (64+ 16) = (80)
AB=AC ಆಗಿರುವುದರಿಂದ ದತ್ತ ಮೂರು ಬಿಂದುಗಳಿಂದ ಉಂಟಾಗಿರುವ ತ್ರಿಕೋನವು ಸಮದ್ವಿಬಾಹು ತ್ರಿಕೋನ |
|
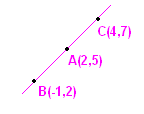
ಸಮಸ್ಯೆ 3: ದೂರದ ಸೂತ್ರವನ್ನು ಉಪಯೋಗಿಸಿ A(2,5), B(-1,2) ಮತ್ತು C(4,7) ಬಿಂದುಗಳು ಏಕ ರೇಖಾಗತ ಎಂದು ತೋರಿಸಿ.
|
ಸೂಚನೆ: BA+AC = BC ಎಂದು ತೋರಿಸಿ (ಆನಂತರ ಬಿಂದುಗಳನ್ನು ಸೇರಿಸಿ ಅವು ಏಕ ರೇಖಾಗತ ಎಂದು ತೋರಿಸಿ) |
|
ಸಮಸ್ಯೆ 4: ಒಂದು ತ್ರಿಕೋನ ABC ಯ ಮೂರು ಶೃಂಗಬಿಂದುಗಳು A(4,6),B(0,4) ಮತ್ತು C(6,2) ಆಗಿದ್ದರೆ ಅದರ ಪರಿಕೇಂದ್ರದ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
|
ಸೂಚನೆ: Let O(x,y) ಪರಿಕೇಂದ್ರವಾಗಿರಲಿ. ಆಗ OA=OB=OC ಮತ್ತು ಆದುದರಿಂದ OA2 = OB2 =OC2 ಪರಿಹಾರ: OA2 = (x-4)2+(y-6)2=x2-8x+16+y2-12y+36 OB2 = (x-0)2+(y-4)2=x2+y2-8y+16 OC2 = (x-6)2+(y-2)2=x2-12x+36+y2-4y+4 OA2 = OB2 ಆಗಿರುವುದರಿಂದ 2x+y =9 OA2 = OC2 ಆಗಿರುವುದರಿಂದ x-2y = -3 ಮೇಲಿನ ಎರಡು ಸಮೀಕರಣಗಳನ್ನು ಬಿಡಿಸಿದಾಗ x=3 ಮತ್ತು y=3 ಆಗಿರುತ್ತದೆ. ಆದುದರಿಂದ O(3,3) ಯು ABC ಯ ಪರಿಕೇಂದ್ರ. |
|
ದತ್ತ ಅನುಪಾತದಲ್ಲಿ ರೇಖೆಯನ್ನು ವಿಭಜಿಸುವುದು
ಭಾಗ ಪ್ರಮಾಣ ಸೂತ್ರ:
ಒಂದು ಸರಳರೇಖೆಯನ್ನು ನೀಡಿದ ಅನುಪಾತದಂತೆ ವಿಭಜಿಸುವ ಬಿಂದುವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರದ ಕುರಿತು ಇಲ್ಲಿ ಕಲಿಯಲಿದ್ದೇವೆ.
|
AB ಯು A (x1, y1) ಮತ್ತು B(x2, y2) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ಸರಳರೇಖೆಯಾಗಿರಲಿ. AB ಯನ್ನು ನೀಡಿದ m1:m2 ಅನುಪಾತದಲ್ಲಿ ವಿಭಜಿಸುವ P(x, y) ಬಿಂದುವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿದೆ A, P ಮತ್ತು B ಗಳಿಂದ x-ಅಕ್ಷಕ್ಕೆ ಎಳೆದ ಲಂಬಗಳು x- ಅಕ್ಷವನ್ನು C,Q ಮತ್ತು D ಗಳಲ್ಲಿ ಕ್ರಮವಾಗಿ ಸಂಧಿಸಲಿ. A ಮತ್ತು P ಗಳಿಂದ x-ಅಕ್ಷಕ್ಕೆ ಎಳೆದ ಸಮಾನಾಂತರ ರೇಖೆಗಳು PQ ಯನ್ನು E ಯಲ್ಲಿ ಮತ್ತು BD ಯನ್ನು R ನಲ್ಲಿ ಸಂಧಿಸಲಿ. If P ಬಿಂದುವು AB ಯನ್ನು m1:m2 ಅನುಪಾತದಲ್ಲಿ ವಿಭಜಿಸಿದರೆ ಆಗ AP/PB = m1/m2 ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿದಂತೆ AEP ಮತ್ತು PRB ಸಮರೂಪಿ ತ್ರಿಕೋನಗಳು (ಕೋ.ಕೋ.ಕೋ ಸ್ವಯಂಸಿದ್ಧ). AE/PR = PE/BR=AP/PB = m1/m2 --------à(1) AE = OQ-OC = x-x1 : PR = OD-OQ = x2-x PE = QP-QE(=CA) = y-y1 BR = DB-DR = y2-y ಈ ಬೆಲೆಗಳನ್ನು (1) ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ AE/PR = (x-x1)/(x2-x) = PE/PR = (y-y1)/ (y2-y) = m1/m2 --------à(2) (x-x1)/(x2-x) = m1/m2 m2(x-x1) = m1(x2-x) (ಅಡ್ಡ ಗುಣಾಕಾರ) m2x - m2x1 = m1x2- m1x (ಬಿಡಿಸಿದಾಗ) x(m2+m1) = m1x2+ m2x1(ಪಕ್ಷಾಂತರದಿಂದ) x = (m1x2+ m2x1)/(m2+m1)(ಭಾಗಿಸಿದಾಗ) ಅದೇ ರೀತಿ (2) ರಿಂದ y = (m1y2+ m2y1)/(m2+m1) A(x1, y1) ಮತ್ತು B(x2, y2) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖೆಯನ್ನು P ಯು m1:m2 ಅನುಪಾತದಲ್ಲಿ ಕಡಿಯುವುದಾದರೆ ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು : {(m1x2+ m2x1)/(m1+m2), (m1y2+ m2y1)/(m1+m2) } ಇದೇ ಭಾಗ ಪ್ರಮಾಣ ಸೂತ್ರ ‘section formula’. |
|
1. AB ರೇಖೆಯ ಮಧ್ಯಬಿಂದುವಿನ(m1:m2 = 1:1) ನಿರ್ದೇಶಾಂಕಗಳು ಯಾವುವು?
ಅದು {(x2+x1)/2), (y2+ y1)/2}: (ಮಧ್ಯ ಬಿಂದು ಸೂತ್ರ)
ಗಮನಿಸಿ: ಮೇಲಿನ ಸೂತ್ರವನ್ನು ಉಪಯೋಗಿಸಿ ಯಾವುದೇ ಚತುರ್ಭುಜದ ಮಧ್ಯಬಿಂದುಗಳನ್ನು ಸೇರಿಸಿದಾಗ ದೊರಕುವ ಚತುರ್ಭುಜವು ಸಮಾನಾಂತರ ಚತುರ್ಭುಜ ಎಂದು ಸಾಧಿಸಬಹುದು
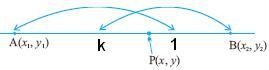
2. ಒಂದು ರೇಖೆಯನ್ನು k:1 ಅನುಪಾತದಲ್ಲಿ ವಿಭಜಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು ಯಾವುವು?
ಅವು : {(kx2+x1)/(k+1), (ky2+ y1)/(k+1)}
ಸಮಸ್ಯೆ 5: A(15,5) ಮತ್ತು B(9,20) ಗಳನ್ನು ಸೇರಿಸುವ ರೇಖೆಯ ಮೇಲಿನ P(11,15) ಬಿಂದುವು ಆ ರೇಖೆಯನ್ನು ಯಾವ ಅನುಪಾತದಲ್ಲಿ ವಿಭಜಿಸಿದೆ?
ಪರಿಹಾರ:
|
P ಯು AB ಯನ್ನು k:1 ಅನುಪಾತದಲ್ಲಿ ವಿಭಜಿಸಲಿ. x1=15, y1=5, x2=9, y2=20,x=11, y=15 ಮೇಲೆ ತಿಳಿಸಿದಂತೆ, ಒಂದು ರೇಖೆಯನ್ನು k:1 ಅನುಪಾತದಲ್ಲಿ ವಿಭಜಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು {(kx2+x1)/(k+1), (ky2+ y1)/(k+1)} x = (kx2+x1)/(k+1), y = (ky2+ y1)/(k+1) x = 9k+15/(k+1) 11 = 9k+15/(k+1)( x=11 ದತ್ತ) 11k+11 = 9k+15 2k=4 or k=2 ಆದುದರಿಂದ P ಯು ರೇಖೆಯನ್ನು 2:1 ಅನುಪಾತದಲ್ಲಿ ವಿಭಜಿಸಿದೆ. |
|
ಸಮಸ್ಯೆ 6: A(6,-2) ಮತ್ತು B(-8,10) ಗಳನ್ನು ಸೇರಿಸುವ ರೇಖೆಯನ್ನು ಸರಿಯಾಗಿ ಮೂರು ಭಾಗ ಮಾಡುವ ಮಧ್ಯದಲ್ಲಿನ ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿ.
ಸೂಚನೆ:
|
AP=PQ=QB (1:1:1) ಎಂದಿರುವಂತೆ P ಮತ್ತು Q ಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿದೆ. ಈ ಸಮಸ್ಯೆಯನ್ನು ಎರಡು ಹಂತದಲ್ಲಿ ಬಿಡಿಸಬೇಕು: 1. AP:PB = 1:2 ಎಂದಿರುವಂತೆ P(x1,y1) ಕಂಡುಹಿಡಿ. 2. AQ:QB = 2:1 ಎಂದಿರುವಂತೆ Q(x2,y2) ಕಂಡುಹಿಡಿ. ಅವು P (4/3,2) ಮತ್ತು Q (-10/3,6). |
|
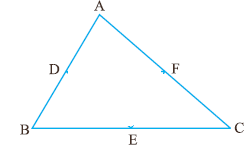
7.2 ಸಮಸ್ಯೆ 7: ತ್ರಿಕೋನ ABC ಯಲ್ಲಿ D(-2,5) ಯು AB ಯ ಮಧ್ಯ ಬಿಂದು. E(2,4) ಯು BC ಯ ಮಧ್ಯ ಬಿಂದು ಮತ್ತು F(-1,2) ಯು AC ಯ ಮಧ್ಯ ಬಿಂದು. A, B ಮತ್ತು C ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿ.
|
ಸೂಚನೆ: A =(x1,y1), B=(x2,y2) ಮತ್ತು C=(x3,y3) ಆಗಿರಲಿ. D(-2,5) ಯು AB ಯ ಮಧ್ಯ ಬಿಂದು ಆಗಿರುವುದರಿಂದ (x1+x2)/2 = -2 ಮತ್ತು (y1+y2)/2 = 5 E(2,4) ಯು BC ಯ ಮಧ್ಯ ಬಿಂದು ಆಗಿರುವುದರಿಂದ (x2+x3)/2 = 2 ಮತ್ತು (y2+y3)/2 = 4 F(-1,2) ಯು AC ಯ ಮಧ್ಯ ಬಿಂದು ಆಗಿರುವುದರಿಂದ (x1+x3)/2 = -1 ಮತ್ತು (y1+y3)/2 = 2 ಈ ಮೂರೂ ಸಮೀಕರಣಗಳನ್ನು ಬಿಡಿಸಿದಾಗ x1= -5, x2=1, x3= 3 y1= 3, y2=7, y3= 1 ಮೂರು ಶೃಂಗಬಿಂದುಗಳು: A(-5,3), B(1,7) ಮತ್ತು C(3,1). |
|
ಕಲಿತ ಸಾರಾಂಶ
|
ಕ್ರ.ಸಂ. |
ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು |
|
1 |
P (x1,y1) ಮತ್ತು Q (x2,y2) ಬಿಂದುಗಳ ನಡುವಿನ ದೂರ = {(x2-x1)2+ (y2-y1)2} |
|
2 |
A(x1,y1) ಮತ್ತು B (x2,y2) ಗಳನ್ನು ಸೇರಿಸುವ ರೇಖೆಯನ್ನು m1:m2 ಅನುಪಾತದಲ್ಲಿ ಕಡಿಯುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು:
|
ಮೂಲ : ಫ್ರೀ ಗಣಿತ
ಕೊನೆಯ ಮಾರ್ಪಾಟು : 1/28/2020